Altın Oran: “Evrenin Matematiği“

Evrende görebileceğimiz tüm nesne ve varlıkların parçaları arasında bir uyumunolduğunu ve binlerce yıldır hiç değişmediği saptandığı için Yaratıcı‘nın matematiksistemi olarak bilinen bağıntıya “altın oran” denilmektedir. Sanatta ve matematikte çok kez karşılaşabileceğimiz bu oran, aslında basit bir kural üzerine oturtulmuştur. Fakat gözlemleyebildiğimiz bütün varlık aleminde bu oranın geçerli ve tutarlı olarak göze çarpması, insanları şaşkına çevirecek kadar ciddi bir sistemi ortaya koyuyor. Evrenin var oluşundan bu yana tutarlı olarak bütün varlıklarda aşağıda açıklanacak olan 1,618′e karşılık gelen bir oranın bulunması, dünyaca ünlü matematikçilerin dehayranlıkla incelediği ve kendi çalışmalarında kullandıkları bir konu alanı olmuştur.

İnsanlık tarihinin başlangıcından beri, evrendeki düzeni keşfetme güdüsü de var olmuştur. Geçen on binlerce yıl içinde yapılan tüm çalışmalar, evrenin alelâde birdüzen içinde yaratılmadığını, hâlâ insan aklının alamayacağı kadar sistematik bir ölçü içerisinde yaratıldığını ortaya koymuştur. Evrenin bu sistemi, kuşkusuz sayılarüzerine oturtulmuştur. Var olan her şey, bir sayıya karşılık gelmektedir. Dil bilimi bile matematiksel kurallar sayesinde gelişimgöstermektedir. Ve biz bu sayıları, daha çok gündelik matematik hesaplamalarında, ölçüp tartmada, mühendislikte ve bunun gibibasit konular üzerinde incelemeye çalışıyoruz. Felsefik boyutta düşünüldüğünde, varoluşun ve doğa yasalarının temelinde de bu sayılar bulunmaktadır. Bu anlamda evrene hâkim olan sayıların yasası, kuşkusuz Tanrı‘nın matematik düzenini ortaya koyacaktır. İştebu düzeni görmemizi sağlayacak anahtar, altın orandır…

İlk olarak kimler tarafından keşfedildiği bilinmese de, Mısırlılar’ın ve Yunanlılar’ın bu konu üzerinde yapmış oldukları bazı çalışmalar olduğu görülmektedir. Öklid, milattan önce 300′lü yıllarda yazdığı “elementler” adlı tezinde “ekstrem ve önemli oranda bölmek” olarak altın oranı ifade etmiştir. Mısırlıların keops piramidinde, Leonardo da Vinci’nin “İlahi Oran” adlı çalışmada sunduğu resimlerde ve aşağıda onlarcası sayılacak nesne ve çalışmalarda kullanıldığı bilinen altın oran, “Fibonacci Sayıları” olarak da bilinmektedir. Orta Çağ’ın en ünlü matematikçisi olan İtalyan kökenli Leonardo Fibonacci, birbiri arasında ardışık ilişki ve olağanüstübir oran bulunduğunu iddia ettiği sayıları keşfetmiştir. Evrendeki muhteşem düzenle birebir örtüşen bu sayıları keşfetmesi nedeniyle, altın orana da adının ilk iki harfi olan “Fi” (Φ) sayısı denilmiştir.

Bilindiği üzere matematikte 3,14 sayısına karşılık gelen ve bir dairenin çevresinin çapına bölümü ile elde edilen “pi” (Π) sayısı bulunmaktadır. Altın oran da, tıpkı pi sayısı (Π) gibi, matematikte 1,618′e eşit olan sabit sayıya verilen addır ve “Fi” (Φ) simgesiylegösterilmektedir. Fi sayısının (Φ), yani altın oranın, bulunabilmesi için temel olarak şu matematik kuralından yararlanılmaktadır:

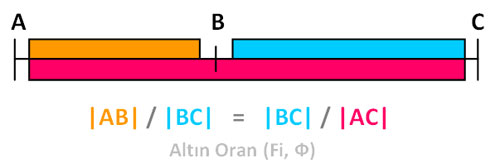
“Bir AC doğru parçası öyle bir B noktasından bölünmelidir ki, küçük parçanın büyük parçaya oranı ile büyük parçanın tüm doğruya oranı birbirine eşit olmalıdır. Yani yukarıdaki doğru parçasından tarif edebileceğimiz üzere, AB küçük parçasının BCbüyük parçasına oranı ile BC büyük parçasının AC doğrusunun tamamına oranı birbirine eşit olmalıdır.” Ayrıca bu kural, “x+1=x²” denkleminden “x²-x-1=0” denkleminin türetilmesini sağlamıştır.

Altın oranın karşılık geldiği 1,618 sayısının matematikteki en şaşırtıcı yanı, tersinin bir eksiğine; karesinin ise bir fazlasına eşit olmasıdır. Bu yönüyle altın oran (Φ) evrende eşi benzeri olmayan, bu özelliğe sahip tek sayıdır. Bu kuralı biraz açarsak, şunları söyleyebiliriz:Bir sayının tersi, o sayının 1′e bölünmesi ile elde edilen sonuçtur. Örneğin 2‘nin tersi 1/2=0,5‘tir. Altın oranın tersi ise, 1 / 1,618 =0,618‘dir. Yani altın oranın tersi, kendisinin 1 eksiğine eşittir. Aynı şekilde altın oranın karesi (1,618)² = 2,618‘e, yani kendisininbir fazlasına eşittir. Bu, şaşkınlık verecek bir durumdur ve bu özellikte başka bir sayı yoktur! Edebiyat Türkçe

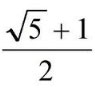Yanda gördüğümüz sayı, altın oranın kısaltılmış biçimini vermektedir. Altın oran, doğadaki tüm varlıklar üzerindegösterilebileceği için, 1,618 değerine ulaşmak sanıldığı kadar zor değildir. Fakat bu oranın sistemini iyice kavrayıp, nesneler üzerinde ona göre bir ölçü belirlemek gerekmektedir. Altın oranın en iyi anlaşılabildiği şekil, altın dikdörtgen denilen ve bir kareden oluşan geometrik biçimdir. Aşağıda bu dikdörtgen üzerinden altın orana nasıl ulaşabileceğimiz gösterilmiştir:

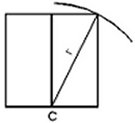1. Adım	2. Adım	3. Adım

4. Adım	5. Adım
6. Adım	Sonuç

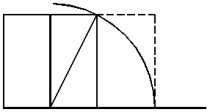
1. Adım: Tüm kenarları birbirine eşit olan bir kare çiziyoruz.

2. Adım: Kareyi, iki eşit dikdörtgene ayıracak biçimde ortadan bölüyoruz.

3. Adım: Dikdörtgenlerin ortak kenarının, karenin tabanını kestiği C noktasına pergelin ucunu koyup, karenin köşesine değecek biçimde bir yay çiziyoruz. Daha sonra yayın kareye değdiği nokta ile C noktasını birleştiriyoruz.

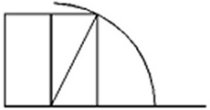
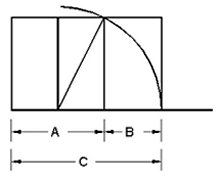
4. Adım: Karenin taban çizgisini, çizdiğimiz yayın devamı ile kesişecek kadar uzatıyoruz. Yay çizgisini de karenin tabanına kadar çekiyoruz.

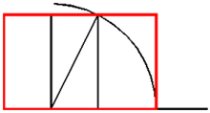
5. Adım: Yay çizgisi ile, karenin tabanının birleştiği noktayı, üçüncü bir dikdörtgenin tabanı olarak düşünüp, ilk karenin köşesinden bunu tamamlıyoruz.

6. Adım: İlk karenin taban uzunluğuna A, en son oluşturduğumuz üçüncü dikdörtgenin taban uzunluğuna B ve ilk kare ile son dikdörtgenin taban uzunluklarının toplamı olan kısmın tamamına C dediğimizde, yazının başında vermiş olduğumuz kuralı uygulayabileceğimiz bir doğru elde edebiliyoruz.

Sonuç: Bu durumda “küçüğün büyüğe oranı” olarak kısaltabileceğimiz altın oranı uygularsak; |B| / |A| = |A| / |C| oranı ortaya çıkacaktır. Dahası uzun kenarın kısa kenara oranı her zaman bize 1,618 (Φ) sayısını verecektir. Yani |A| / |B| = 1,618 (Φ) ve |C| / |A| = 1,618 (Φ) olacaktır. Sonuç olarak elde ettiğimiz dikdörtgen, bir “altın dikdörtgen” olacaktır ve bu dikdörtgenin içindeki herhangi bir yerden çıkarılabilecek tüm kareleri çıkardıktan sonra elimizde kalacak olan dikdörtgen de altın dikdörtgen olacaktır. Bu kurallar, örneği aşağıda gösterilen tüm altın dikdörtgenler üzerinde uygulanabilecektir. 

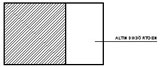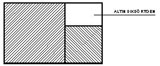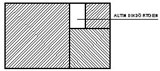Altın dikdörtgenden çıkan karelerden sonra kalan dikdörtgen, yine altın dikdörtgendir.

Altın oran sabit değerini kendi sıralı sayı sistemi içerisinde gösteren İtalyan matematikçi Leonardo Fibonacci, bir gün tavşan çiftliği bulunan bir arkadaşıyla tavşanların yavrulaması üzerine konuşurken, En az iki aylık tavşanların yavruladığını öğrenmiş ve buna göre bir çift tavşanla yola çıkıldığında örneğin 100 ay sonra kaç tavşanın olacağı konusunda tartışmışlardır. Bunu bir matematik formülü ile açıklamaya çalışan Fibonacci, hangi ayı bulmak istiyorsak ondan önceki iki ayı toplayıp sonuca ulaşmamız gerektiği kanısına varmıştır. Ve bu çabası sonucunda kendi adıyla anılan sayıları bulmuştur.

“0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181…”

Yukarıda gösterilen Fibonacci sayıları, kendisinden önceki iki sayının toplamı ile devam etmektedir. Örneğin k sayısı, kendisinden önceki iki sayının (1+1); 13 sayısı da kendisinden önceki iki sayının (5+8) toplamını göstermektedir. “İyi de, peki bu sayıların altın oran ile bağlantısı nedir?” sorusu aklınıza gelebilir, onu da şöyle açıklayalım: Bir Fibonacci sayısının ile kendinden önceki sayıya bölümü ile elde edilen sonuç, 1,618′dir. Örneğin; 987 / 610 = 1,618032… sonucunu vermektedir. Bu durum, 89′dan daha küçük olan Fibonacci sayıları için 0,01 gibi küçük bir farklılıkla ortaya çıksa da, büyük sayıların tamamında sonuç aynıdır.

Altın Oran Hakkında Gelin Bir Video İzleyelim.

http://www.bilgicik.com/yazi/altin-oran-evrenin-matematigi/ alıntı yapılmıştır.